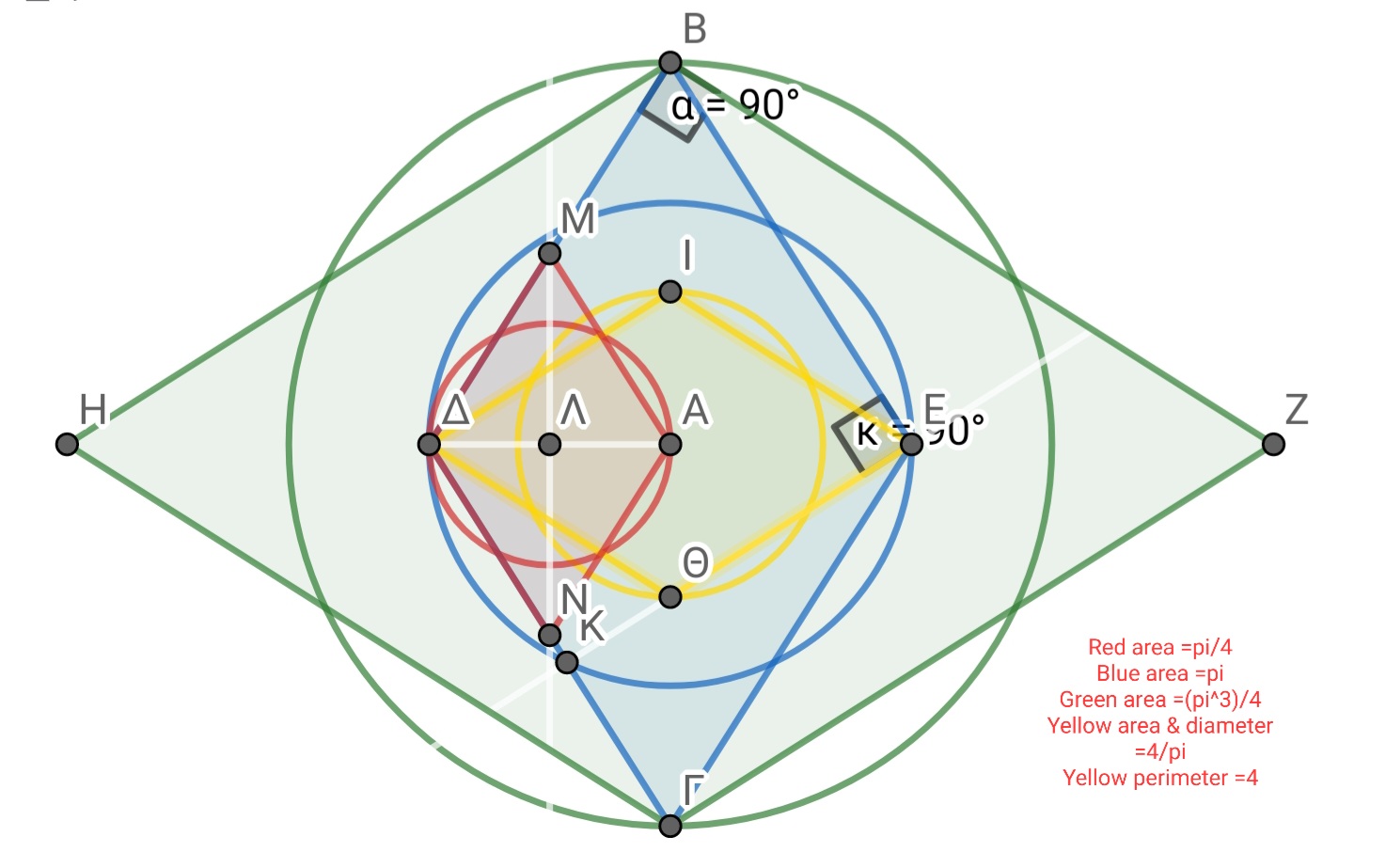
Attempt to square the circle with ruler and compass, according to Euclidean geometry. Hypothesis HA, verification BE.
Work, construction and theory, research. Georgios Bouras.
Perimeter and area of each circle with ruler and compass only
CONSTRUCTION STEPS, METHODOLOGY.
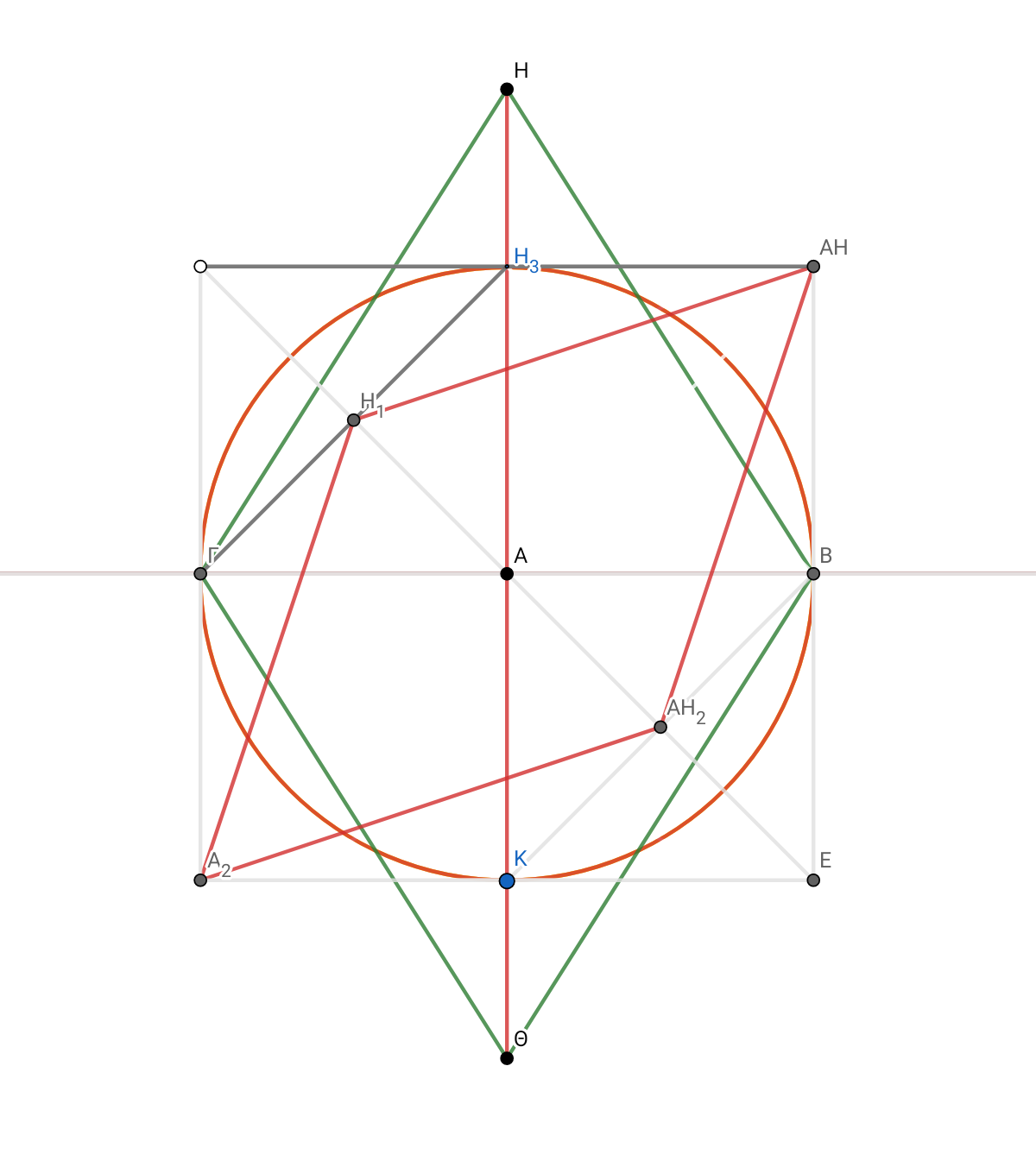
HA^2 = (3/4)^2+(1/4)^2. HA×4=μπ. (ΓB×HΘ)÷2 = area1 = HA. =1/4 μπ I place it perpendicular to ΓB in the center A and correspondingly I place AΘ ... and I have Small diagonal ΓB=1 and large diagonal HΘ= ½ of the circumference of the circle. And I place the sides of the rhombus.
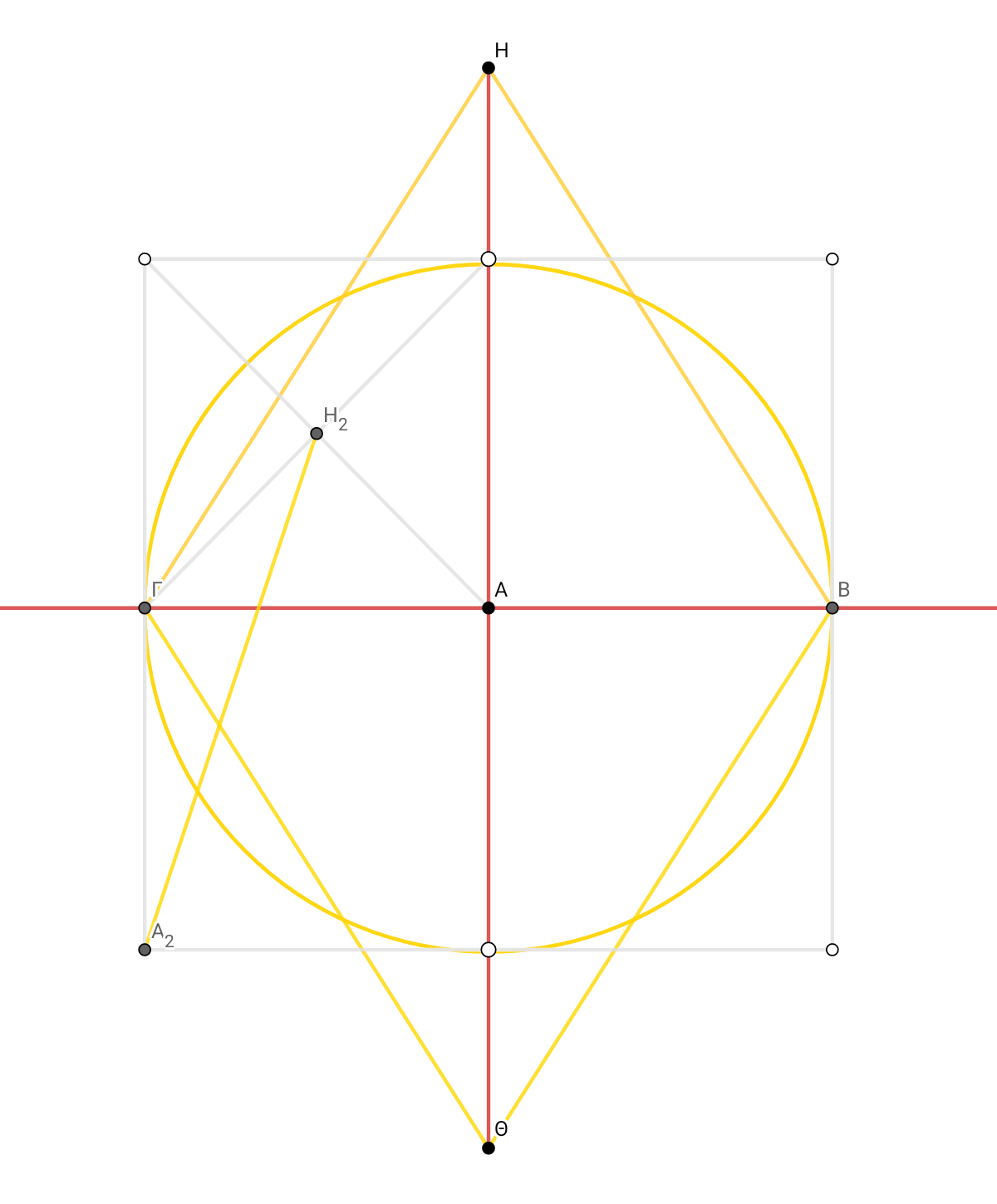
ΓB × √4 = ΓZ. I move the axis and double to ΓZ . I extend ΓH to the vertical axis at M and correspondingly all the sides and double ΗΘ to ΜΠ. ΗΘ × √4 = MΠ. area2=MΠ
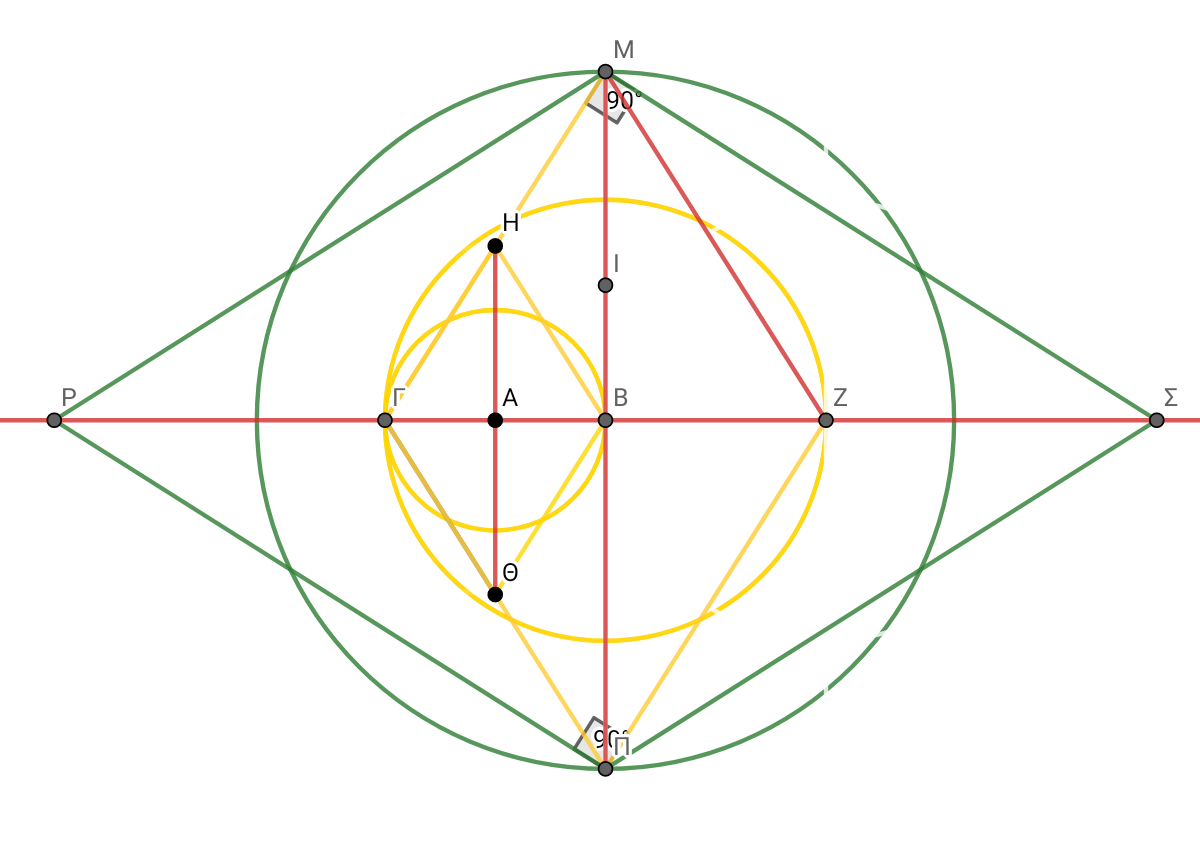
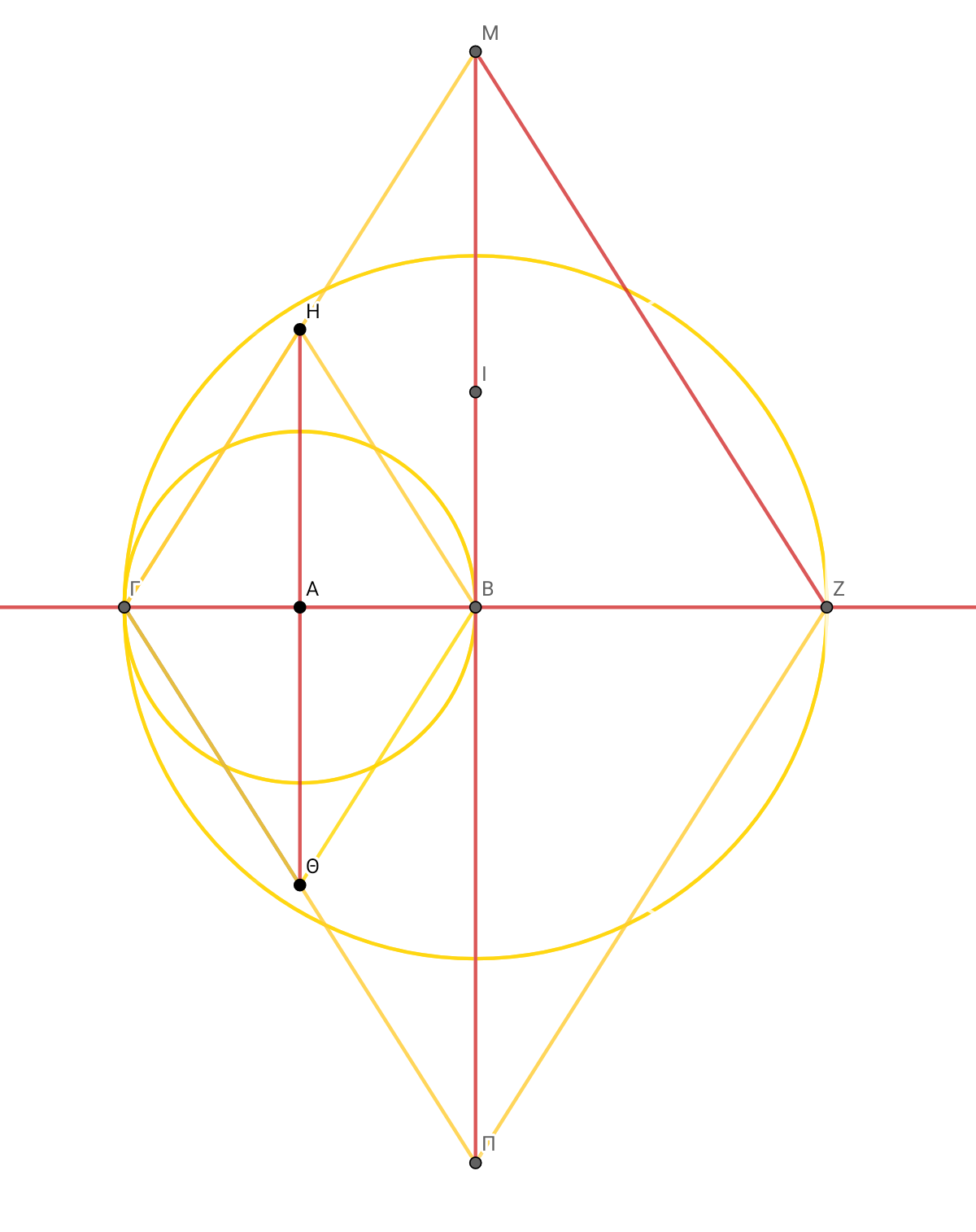
ΜΠ^2/2 = ΡΣ. Area3= ΜΠ×ΜΠ^2)/4 from ΓΜ I bring a perpendicular from M to the horizontal axis to Σ and accordingly draw all its sides
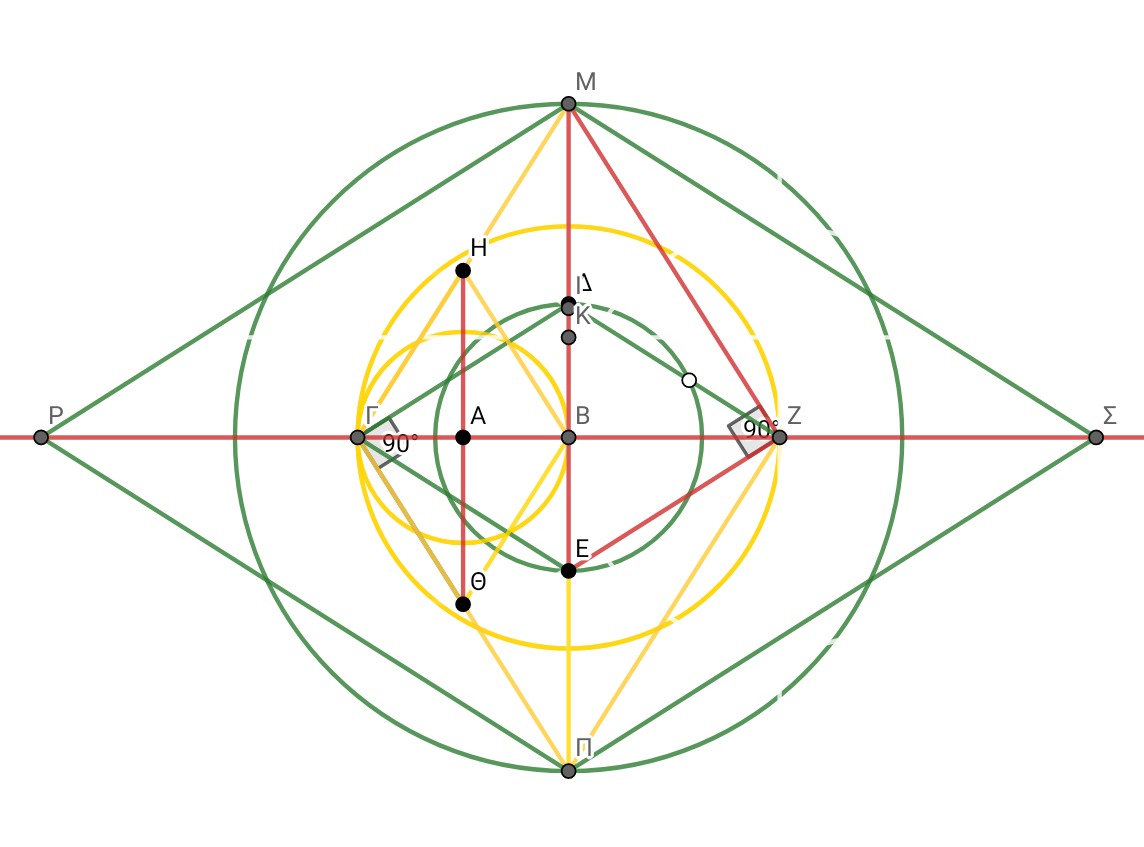
ΜΖ^2= ΜΒ^2 + ΒΖ^2 . ΜΖ^2 ÷ ΜΠ^2/4= ΖΕ^2. ΖΕ^2 - ΒΖ^2 = ΒΕ^2 ΜΠ ÷ √(ΜΠ^2/4)=ΓΖ =2 )και ΓΖ ÷ √(ΜΠ^2/4)=ΚΕ= 2ΓΖ/ΜΠ (of perimeter 4 and an area equal to diameter 4÷MΠ). 2ΓΖ÷ΚΕ=ΜΠ=4ΗΑ. I bring a perpendicular from MZ from Z to the vertical axis at point E and draw a diameter and respectively all the sides.
George Bouras ©
Details and theory at the page theory analysis
Date of creation 2009
Date of first publication on individual blog 01/2010 and Facebook 11/2023
Page issue date 01/2024