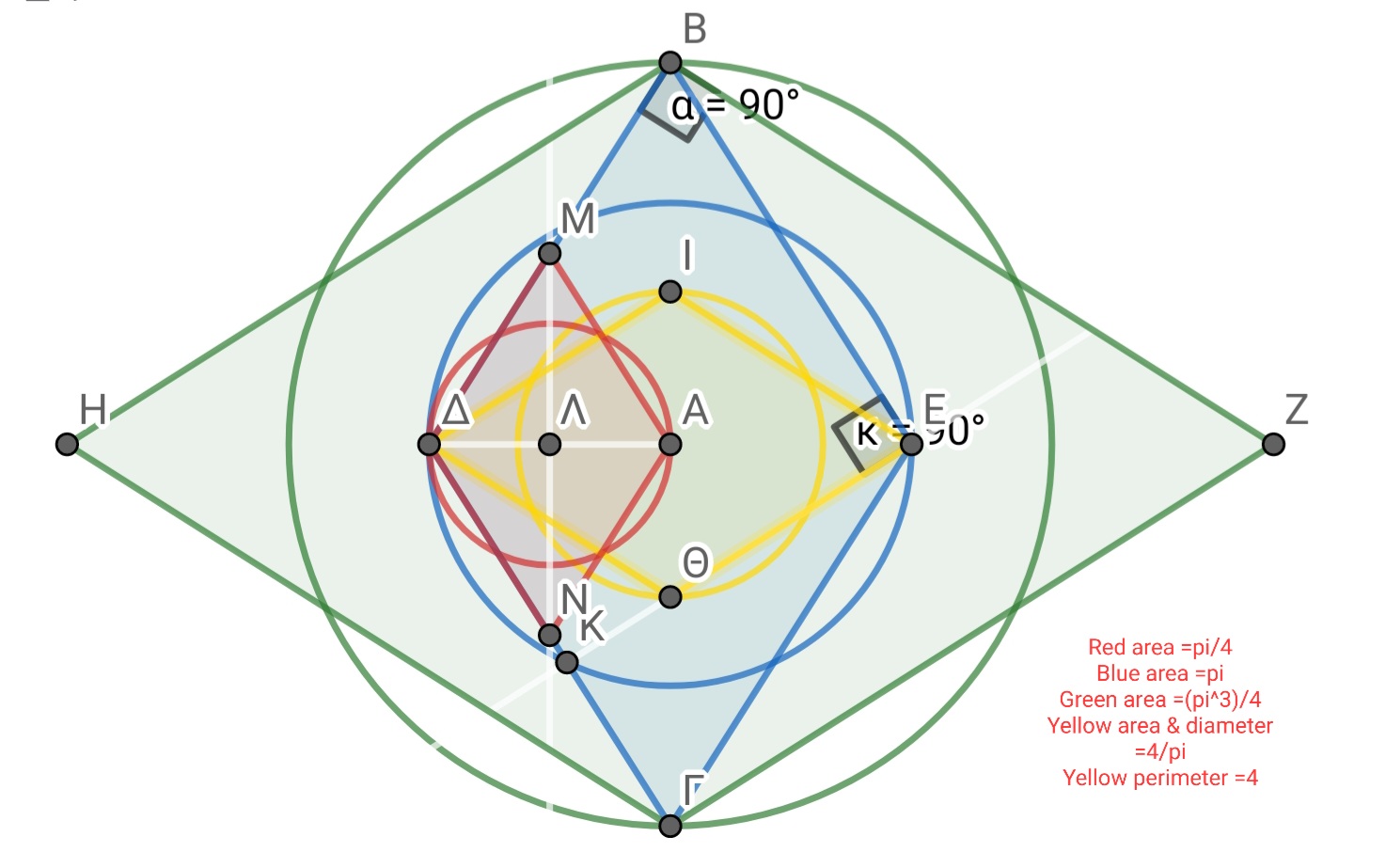
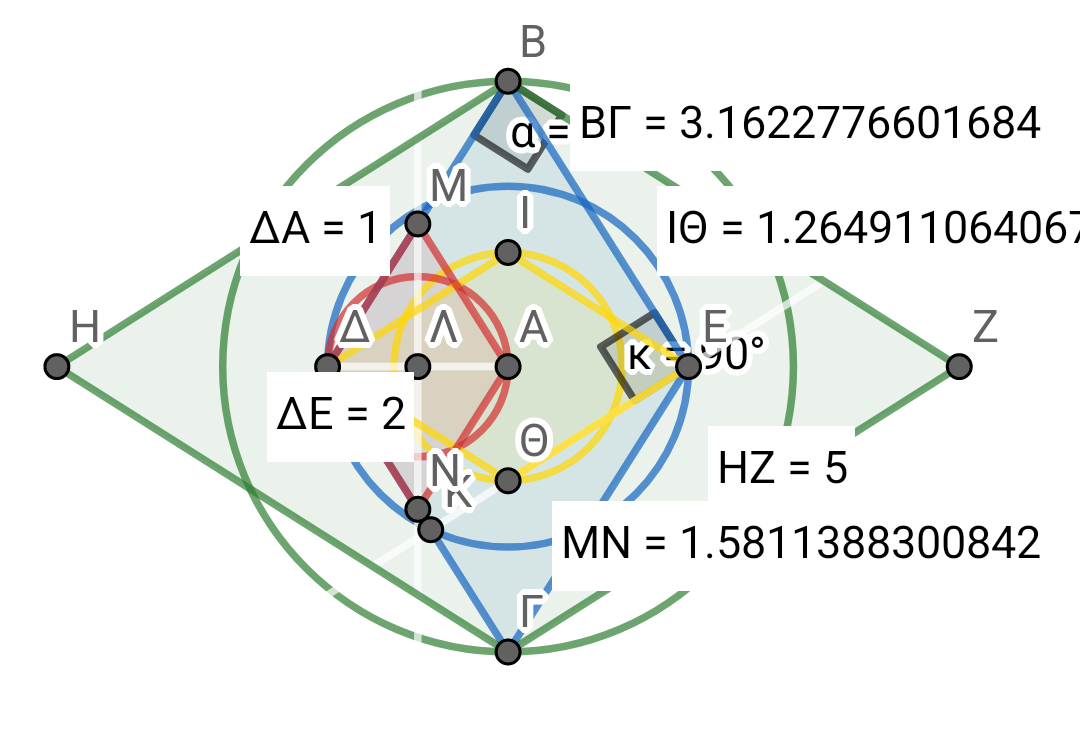
Προσπάθεια τετραγωνισμού του κύκλου με κανόνα και διαβήτη, σύμφωνα με την ευκλείδειο γεωμετρία. Υπόθεση ΗΑ, επαλήθευση ΒΕ.
Εργασία, έρευνα, κατασκευή και θεωρία, Γεώργιος Μπούρας.
Περίμετρος και εμβαδόν κάθε κύκλου μόνο με κανόνα και διαβήτη
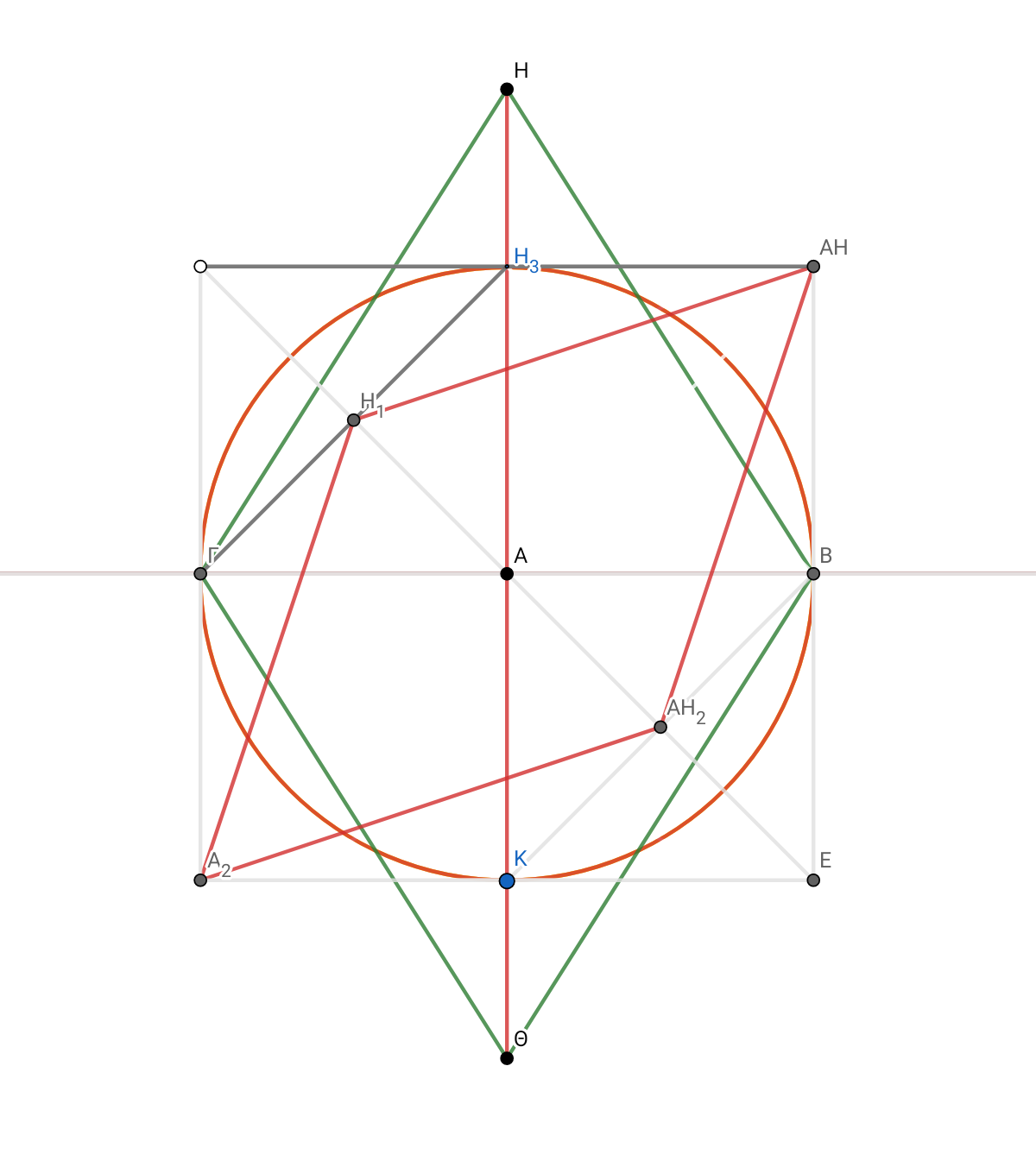
ΒΗΜΑΤΑ ΚΑΤΑΣΚΕΥΗΣ, ΜΕΘΟΔΟΛΟΓΙΑ.
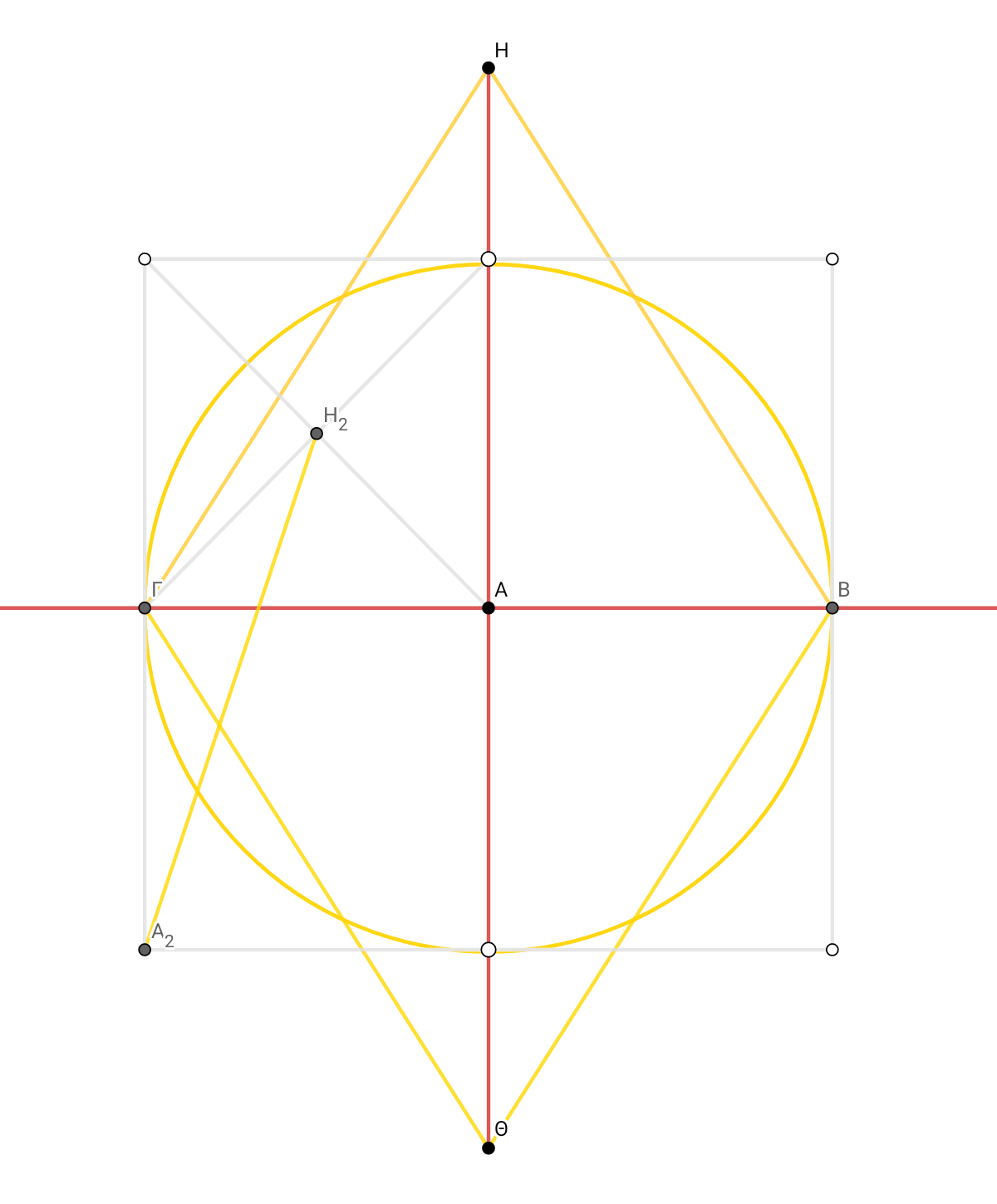
ΗΑ^2 = (3/4)^2+(1/4)^2. ΗΑ×4=μπ. (ΓΒ×ΗΘ)÷2 = Εμ1 = ΗΑ. =1/4 μπ Την τοποθετώ κάθετα στην ΓΒ στο κέντρο Α και αντίστοιχα τοποθετώ την ΑΘ … και έχω Μικρή διαγώνιο ΓΒ=1 και μεγάλη διαγώνιο ΗΘ= ½ περιμέτρου του κύκλου. Και τοποθετώ της πλευρές του ρόμβου.
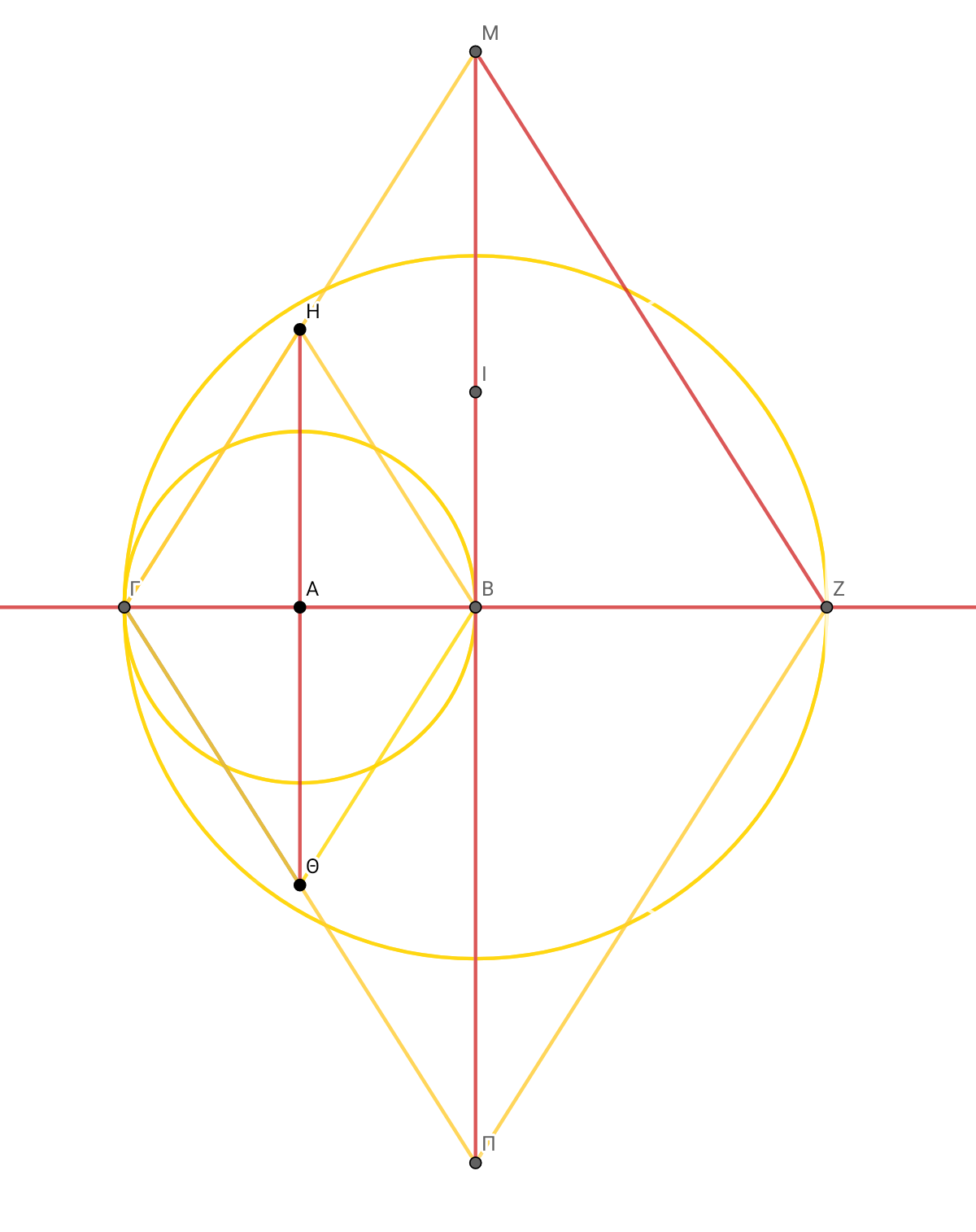
ΓΒ × √4 = ΓΖ. Μεταφέρω τον άξονα και διπλασιάζω σε ΓΖ . Επεκτείνω τη ΓΗ ως τον κάθετο άξονα στο Μ και αντίστοιχα όλες τις πλευρές και διπλασιάζεται η ΗΘ σε ΜΠ ΗΘ × √4 = ΜΠ. Εμ2=ΜΠ
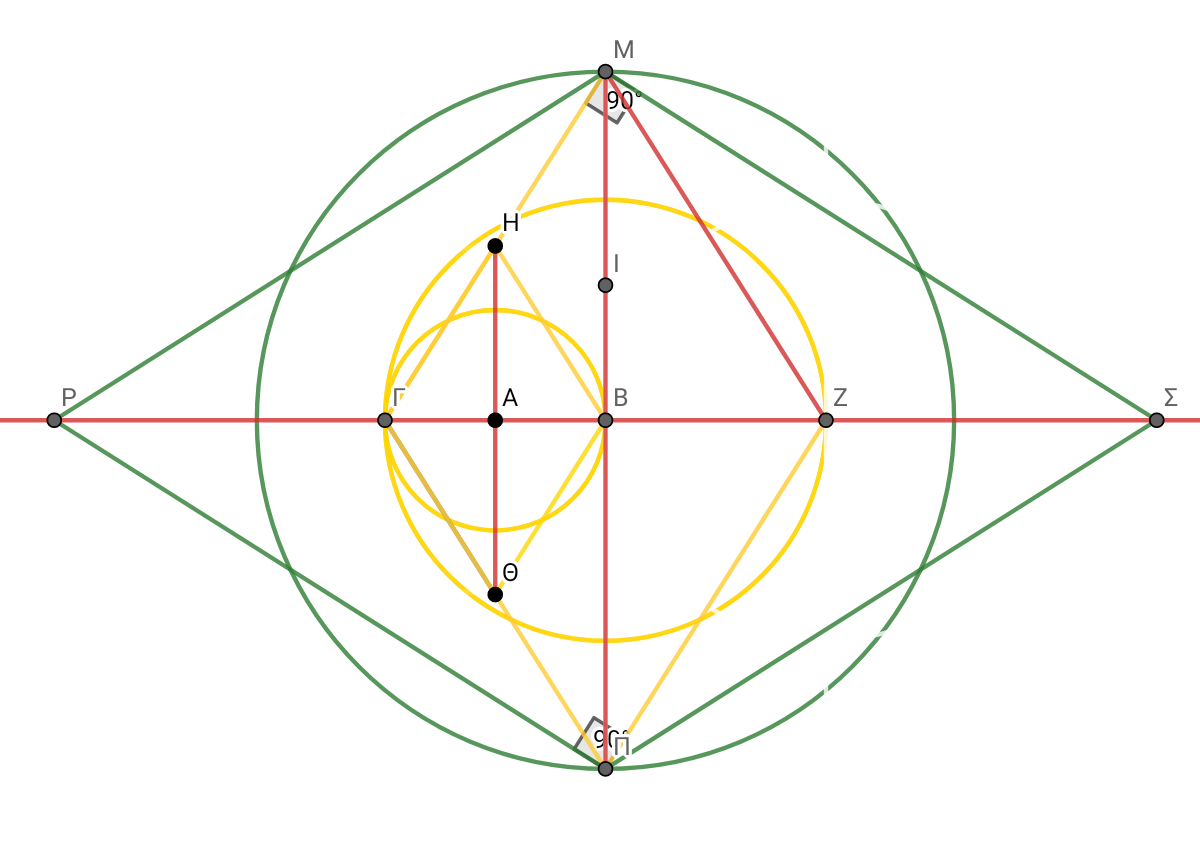
ΜΠ^2/2 = ΡΣ. Εμ3= ΜΠ×ΜΠ^2)/4 Από ΓΜ φέρνω κάθετη από Μ στον οριζόντιο άξονα στο Σ και αντίστοιχα χαράζω όλες της πλευρές
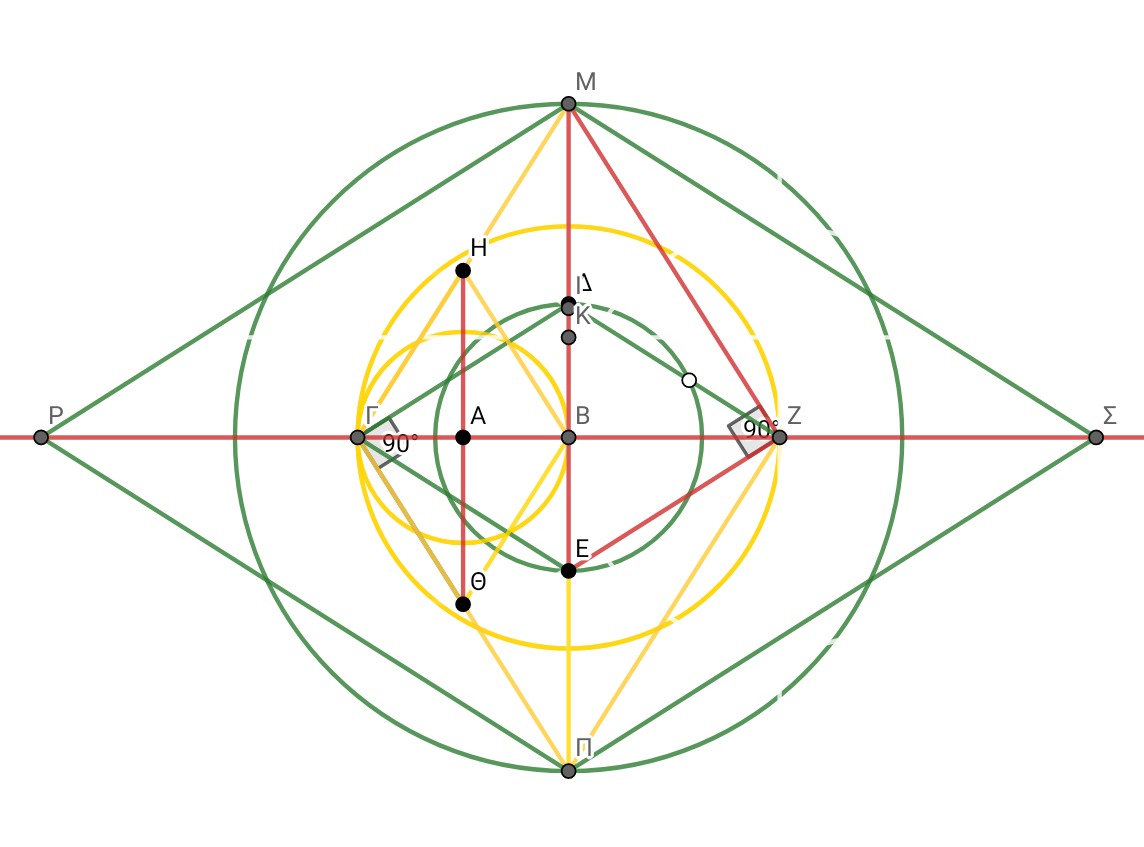
ΜΖ^2= ΜΒ^2 + ΒΖ^2 . ΜΖ^2 ÷ ΜΠ^2/4= ΖΕ^2. ΖΕ^2 - ΒΖ^2 = ΒΕ^2 ΜΠ ÷ √(ΜΠ^2/4)=ΓΖ =2 )και ΓΖ ÷ √(ΜΠ^2/4)=ΚΕ= 2ΓΖ/ΜΠ (περιμέτρου 4 και εμβαδόν ίση με διάμετρο 4÷ΜΠ) 2ΓΖ÷ΚΕ=ΜΠ=4ΗΑ Φέρνω κάθετη από ΜΖ από Ζ στον κάθετο άξονα στο σημείο Ε και χαράζω διάμετρο και αντίστοιχα όλες τις πλευρές.
Γεώργιος Μπούρας ©
Λεπτομέρειες και θεωρία στη σελίδα Θεωρία ανάλυση.
Ημερομηνία δημιουργίας 2009
Ημερομηνία πρώτης έκδοσης σε ατομικό blog 01/2010 και Facebook 11/2023
Ημερομηνία έκδοσης σελίδας 01/2024